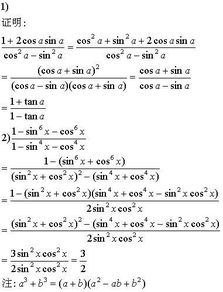恒等式

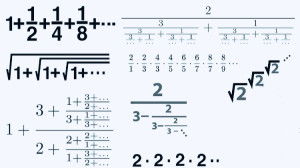
恒等式：数学中的奇妙桥梁

恒等式，作为数学中的一种特殊表达式，承载着数学家们对数学世界的深刻理解和巧妙构思。它揭示了数学中各种概念和公式之间的内在联系，为数学研究提供了丰富的素材和工具。

恒等式的定义与特点

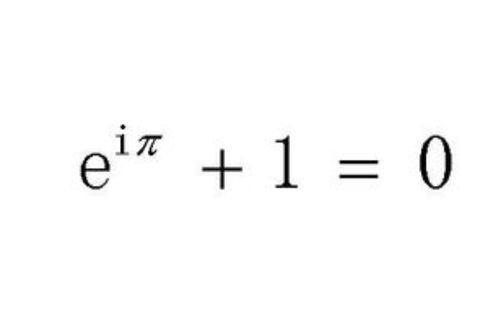
恒等式是指对于所有可能的取值，两个数或表达式始终相等的关系。它具有以下特点：

- 普遍性：恒等式对于所有可能的取值都成立，不受特定条件限制。

- 简洁性：恒等式通常以简洁的形式表达，便于记忆和推导。

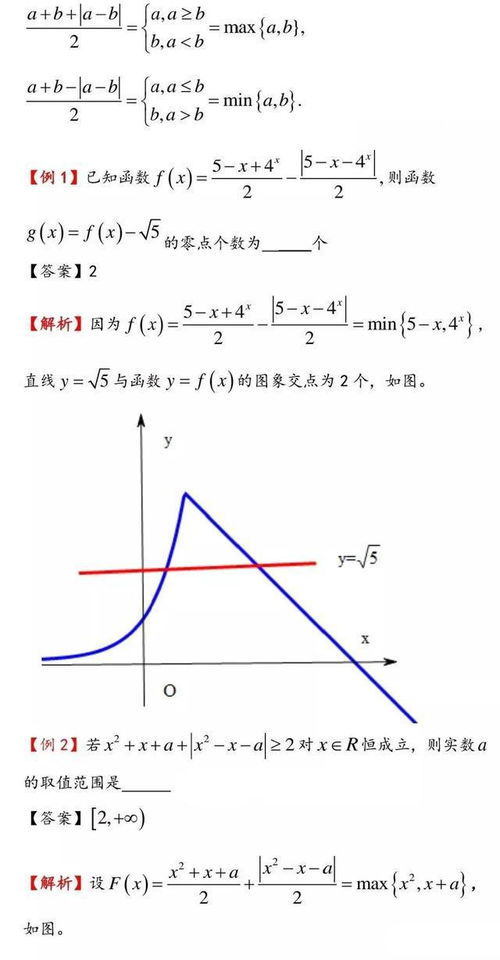
- 实用性：恒等式在数学研究和实际问题中具有广泛的应用。

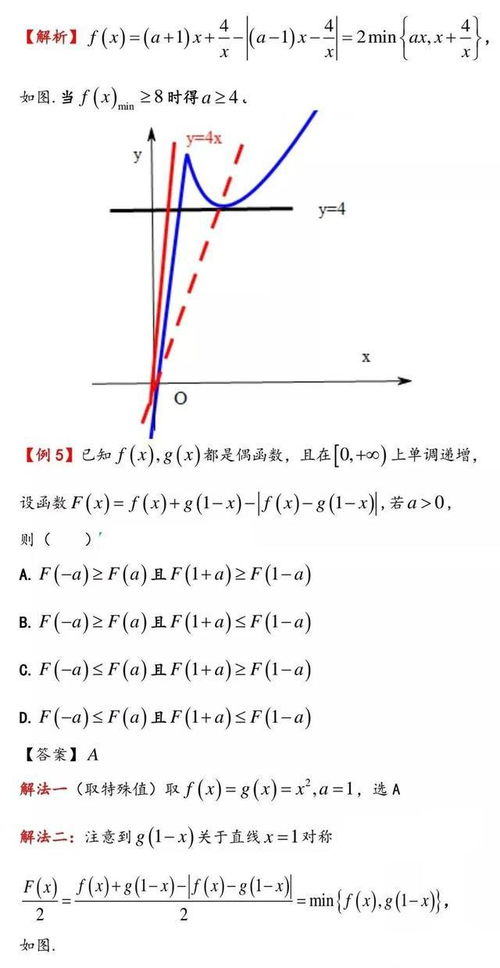
恒等式的证明方法

- 归纳法：通过验证恒等式在特定情况下成立，然后逐步推广到所有情况。

- 反证法：假设恒等式不成立，推导出矛盾，从而证明恒等式成立。

- 构造法：构造一个满足恒等式的具体例子，证明该例子满足恒等式，从而证明恒等式成立。

- 三角恒等式：利用三角函数的性质和关系进行证明。

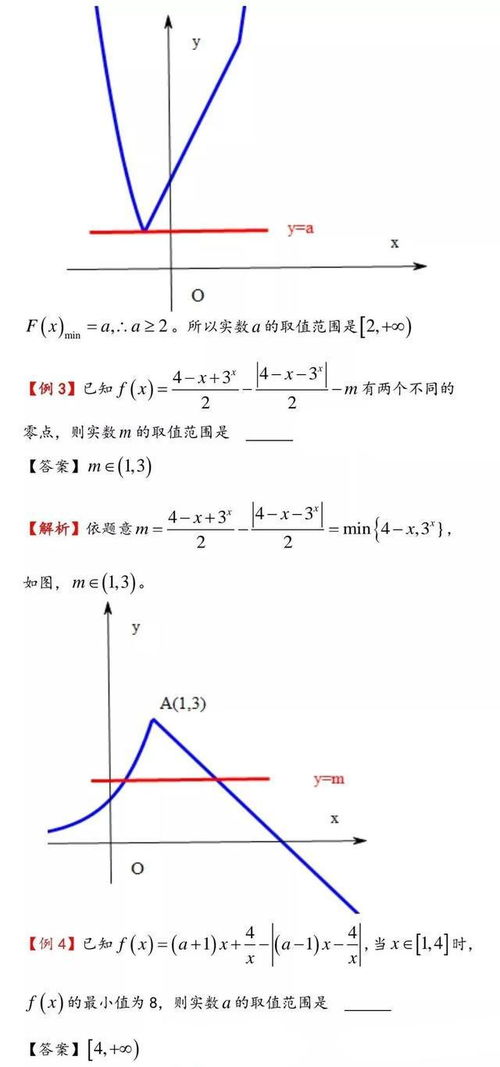
恒等式的应用

- 微积分：恒等式在微积分中用于简化积分和微分运算。

- 线性代数：恒等式在线性代数中用于求解线性方程组和矩阵运算。

- 概率论：恒等式在概率论中用于计算概率和期望值。

- 工程问题：恒等式在工程问题中用于分析和设计。

著名的恒等式

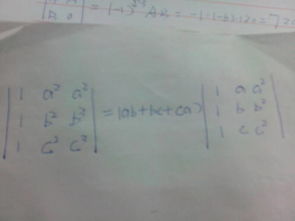
- 欧拉公式：\\( e^{i\\pi} 1 = 0 \\)

- 勾股定理：\\( a^2 b^2 = c^2 \\)

- 二项式定理：\\( (a b)^n = \\sum_{k=0}^{n} \\binom{n}{k} a^{n-k} b^k \\)

- 拉马努金恒等式：\\( \\sum_{n=1}^{\\infty} \\frac{1}{n^2} = \\frac{\\pi^2}{6} \\)

恒等式与数学之美

- 简洁性：恒等式的简洁形式体现了数学的简洁之美。

- 统一性：恒等式将不同的数学概念和公式统一起来，体现了数学的统一之美。

- 和谐性：恒等式中的各个部分相互协调，体现了数学的和谐之美。

恒等式是数学中的一种特殊表达式，它承载着数学家们对数学世界的深刻理解和巧妙构思。恒等式在数学研究和实际问题中具有广泛的应用，是数学之美的体现。通过学习和研究恒等式，我们可以更好地理解数学，感受数学的魅力。